Gelegentlich habe ich den Bedarf, in WordPress Formeln zu schreiben, dass soll ja bei Mathematikern so eine Berufskrankheit sein.
Dazu verwende ich natürlich LaTeX (what else) und möchte hier gerade einen Testblog mit eingebettetem LaTeX Code zeigen. Es gibt mehrere LaTeX Plugins für WordPress; hier teste ich QuickLaTeX. In einem früheren Blog habe ich verschiedene Möglichkeiten vorgestellt, die Bilder im Blog waren aber nur als fertige Bilder manuell eingebettet worden. Jetzt wollen wird diese Bilder wirklich durch das Plugin erzeugen lassen: QuickLaTeX compiliert den LaTeX- Code beim Aufruf der Seite in eine Grafik (mit einem online Web Service) und cached sie auf der WordPress Seite.
Also ein paar echte Beispiele, wie sie ohne weitere Bearbeitung durch das Plugin gerendert werden. Gerade bei speziellen Schriften (hier: Mengensymbole mit Doppelstamm im dritten Beispiel) zeigen sich Darstellungsfehler – mit etwas Überarbeitung wird auch das wieder gut sein. Soll mir ja niemand mit Word kommen….
Euler-Poincaré-Charakteristik eines Kettenkomplexes
Unter einem endlichen Kettenkomplex C versteht man eine Folge von Homomorphismen
![]()
mit der Eigenschaft ![]() , d.h.
, d.h. ![]() . Der Quotientenvektorraum
. Der Quotientenvektorraum
![]()
heisst die i-te Homologie des Komplexes. Man beweise: Sind alle ![]() endlichdimensonal, so gilt:
endlichdimensonal, so gilt:
![]()
Bemerkung: diese Wechselsumme heisst Euler-Poincaré-Charakteristik des Komplexes ![]() und wird mit
und wird mit ![]() bezeichnet.
bezeichnet.
Bilder mit tikz/pgfplots
Mit etwas Umstellungen im Code können auch Bilder mit tikz berechnet werden.
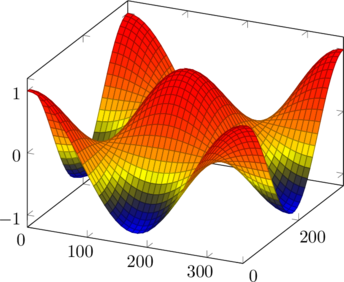
Symplectic mappings of Sobolev Class
Let ![]() ,
, ![]() , be a domain.
, be a domain.
A mapping ![]() is symplectic (with respect to the standard symplectic form
is symplectic (with respect to the standard symplectic form ![]() ) if
) if
(1) ![]()
The symplectic mappings are special mappings of finite dilatation and thus are covered by the following main theorem.
Let ![]() be a mapping of finite dilatation. Then
be a mapping of finite dilatation. Then
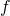 has a continuous representative (also called
has a continuous representative (also called 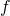 ) satisfying
) satisfying
![Rendered by QuickLaTeX.com \[|f(x)-f(y)| \le C(n)||Df||_{L^n}\left(\log\frac{2}{|x-y|}\right)^{-1/n}\quad x,y\in K\subset\Omega\textrm{ compact},\]](http://ec2-52-29-166-97.eu-central-1.compute.amazonaws.com/myblog/wp-content/ql-cache/quicklatex.com-fc5f7916888d467a8cafd9e94dfbdd8c_l3.png)
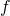 is differentiable pointwise almost everywhere in the ordinary sense,
is differentiable pointwise almost everywhere in the ordinary sense,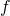 satisfies Lusin’s conditions
satisfies Lusin’s conditions 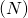 and
and 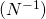 , i.e. the image of a set with zero Lebesgue
, i.e. the image of a set with zero Lebesgue 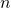 -measure is a set of zero measure and also the preimage of a zero-set is a zero-set.
-measure is a set of zero measure and also the preimage of a zero-set is a zero-set.
Ein Gedanke zu „Test QuickLaTeX“
Hej Andreas. Superseite und staune über Deine vielen Hobbys!
Gruss aus OZ es vy 73
Christoph HB9AJP / OZ8AP