Die 5 Würfel seien zur einfacheren Unterscheidung farbig. Die Zahlen auf auf ihnen sind wie folgt gewählt. Man beachte, dass die Augensumme wie bei einem normalen Würfel immer 21 beträgt.
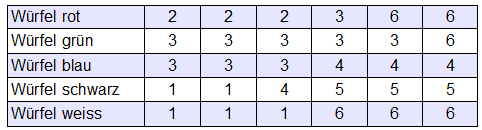
Ein Spieler gewinnt, wenn er eine höhere Augenzahl wirft als sein Gegner; dies ist wichtig, denn die Unentschieden mit der gleichen Augenzahl werden nicht gezählt. Die Gewinnwahrscheinlichkeiten müssen deshalb für beide Spieler zusammengezählt nicht 100% ergeben!
Die zweite Zutat des Rätsel ist die Tatsache, dass für die Berechnung der Gewinnwahrscheinlichkeiten immer ein Paar Würfel betrachtet werden muss, für einen einzelnen Würfel ist eine Gewinnwahrscheinlichkeit nicht definiert. Ein Beispiel mit dem roten und dem grünen Würfel: von allen möglichen Würfen (6×6=36 Fälle) gewinnt rot in 10 Fällen, nämlich nur, wenn er eine der beiden 6 wirft. Grün gewinnt dagegen in 5×3+4=21 Fällen. Der grüne ist also mehr als „doppelt so gut“ wie der rote. Wir könnten verleitet sein, zu sagen, dass er eine „Güte“ grösser 2 hat.
Dies kam man jetzt weiterrechnen: blau ist besser als grün, schwarz besser als blau, weiss besser als schwarz und – man staune – rot ist besser als weiss! Immer wenn der Banker einen Würfel wählt, kann der Mathematiker einen besseren nehmen, und zwar reihum! Wichtig ist natürlich, dass der Banker zuerst wählt und nicht allzu gut rechnet (gewisse Parallelen zum realen Leben sind da). Mit dem Begriff der „Güte“ kommen wir aber in Schwierigkeiten…
Merke:
- nicht jede Eigenschaft eines Gegenstandes kann mit einer Zahl gemessen werden, manchmal sind die Verhältnisse zu anderen Objekten zu beachten
- nicht jede Objekt kann mit einer Eigenschaft linear geordnet werden, es gibt nicht immer ein „bestes Objekt“
- eine „Performance-Optimierung“ ist meist eine krude, im wörtlichen Sinn eindimensionale Sicht der Wirklichkeit
Im Sinne dieser philosophischen Predigt wünsche ich allen Lesern ein vielschichtiges und vielfältiges neues Jahr !