Im Estrich oben drückt der Elektriker die Drähte in eine Reihe flach auf den Boden und verbindet die Enden paarweise – es gibt 5 Paare und der 11. Draht bleibt also unverbunden. Er geht in den Keller, findet mit dem Durchgangsprüfer heraus, welche Drähte Paare sind und schreibt sie mit A1, A2, B1, B2, C1, C2, D1, D2, E1, E2 an. Der 11. Draht bleibt alleine übrig und wird mit F angeschrieben. Dann verbindet er die Enden im Keller wie in der folgenden Zeichnung:

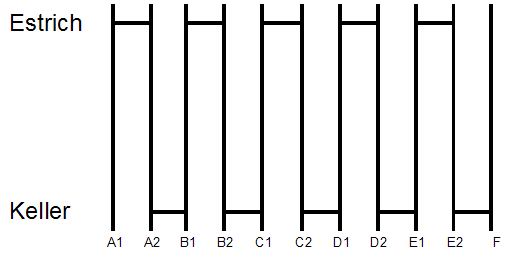
Er geht wieder hinauf und löst alle Drähte voneinander, aber so, dass er noch weiss, welche Paare zusammengehörten. Er prüft den Durchgang vom 11. Draht (er weiss bereits, dass es das obere Ende von F ist) zu allen andern – nur einer hat Kontakt, nämlich E2. Sein Partner ist also E1. Beide werde angeschrieben. Nun prüft er den Durchgang von E1 – nur D2 hat Kontakt. Sein Partner ist also D1. Nun prüft er den Durchgang von D1 – nur C2 hat Kontakt. Sein Partner ist also C1 usw. So kann er der Reihe nach alle Enden bestimmen. Das Verfahren funktioniert für eine beliebige ungerade Anzahl von Drähten und mit einer Zusatzüberlegung – die hier nicht verraten sei – auch für gerade Anzahlen (ausser bei 2 Drähten).

Neues Quiz

Wir haben 3 Gefässe mit 8, 5, und 3 Liter Inhalt. Frage: wie können wir genau 4 Liter durch Umgiessen abmessen? Die Gefässe tragen keine Markierungen und sind undurchsichtig (aus Blech). D.h. man kann ein Gefäss immer nur ganz ausgiessen oder ein anderes bis zum Rand füllen, aber nicht halb leeren.

Diese Frage lässt sich mit etwas Tüfteln lösen. Es gibt jedoch einen physikalischen resp. mathematischen Hintergrund, der bei der Lösung solcher und ähnlicher Fragen behilflich ist. Wer eine Theorie kennt oder eine Idee hat, kann sich auch an der folgenden Zusatzfrage versuchen: Können wir mit 3 Gefässen mit 8, 7, 6 Liter Inhalt auch 5 Liter abmessen?